いろいろ σ1/n^2=π^2/6 147646-σ1/n^2=π^2/6

The American Mathematical Monthly 115(8)If f(x)=(πIxI) 2 on π,π, prove that f(x)=π 2 /3 Σ(4 cos nx/n 2) and deduce that Σ1/n 2 =π 2 /6 , Σ1/n 4 =π 4 /90 Note; Cos^2 π/6In today's blog, I show the proof that ∑ 1/n 2 = π 2 /6 For background on Basel's problem and Leonhard Euler's technique for arriving at the solution, see here In today's blog, I show a proof that Euler's solution is correct Most of the content in today's blog is taken from the Wikipedia article on the Basel Problem See references

Testing The Convergence Of Sum Limits N 1 Infty Frac N Pi N E N 2 Mathematics Stack Exchange

σ1/n^2=π^2/6

σ1/n^2=π^2/6- Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeCos（iy）＝1＋1／6y^2＋1／1y^4＋・・・＝cosh（y） という双曲関数が得られます． 同様に，実軸上の単項式x^nを単項式z^nに解析接続し，それを単位円周上に制限すると このように実解析関数の変数を複素数に拡張すること

Emt4801 Tut102 For Year19 Memo 1 2 3 4 Pdf 1 Assignment 01 Emt4801 102memo 0 19 2 Solution To Question 1 I A Consider Un U N 1 N Nn It Course Hero

In mathematics, Gelfond's constant, named after Aleksandr Gelfond, is e π, that is, e raised to the power πLike both e and π, this constant is a transcendental numberThis was first established by Gelfond and may now be considered as an application of the Gelfond–Schneider theorem, noting that = = (), where i is the imaginary unitSince −i is algebraic but not rational, e π is Σ 1/(2n 1)²是奇数项的和，如果从原来那个和减去这项，就会得到偶数项。 Σ 1/n² = Σ 1/(2n)² Σ 1/(2n 1)²，右边，前一项是偶数项，後一项是奇数项De Moivre's theorem gives a formula for computing powers of complex numbers We first gain some intuition for de Moivre's theorem by considering what happens when we multiply a complex number by itself Absolute value r = a 2 b 2 Argument θ subject to cos ⁡ θ = a r, sin ⁡ θ = b r

Vienāda nosaukuma trigonometrisko funkciju vienādības nosacījumi Vienādība sinα = sinβ ir spēkā tad un tikai tad, ja α=β2πn vai α=πβ2πn, n∈Z; と計算したのですが、答えは (π^2)/6 のようです。 何が間違っているのかまったく分からない状態です。 分かる方いらっしゃいましたら是非教えてください。標題 Fw Σ1/n^2 = (π^2)/6 時間 Wed Jul 23 14 ※ 本文轉錄自 Dirichlet 信箱 作者 email protected ("Weak and only weak") 標題 Σ1/n^2 = (π^2)/6 時間 Wed Jul 23 14 作者 pretend (Nature Weak) 站內 pretend 標題 Σ1/n^2 = (π^2)/6 時間 Sun Dec 26 04 來介紹一個很漂亮的

Vienādība cosα = cosβ ir spēkā tad un tikai tad, ja α=β2πn vai α=β2πn, n∈Z;この公式により右辺の各項の積分はほとんど 0 0 0 になり， ∫ 0 T a n cos ⁡ 2 2 π n x T d x = a n 2 T \displaystyle\int_0^Ta_n\cos^2\dfrac{2\pi nx}{T}dx=\dfrac{a_n}{2}T ∫ 0 T a n cos 2 T 2 πn x d x = 2 a n T だけが生き残ります。 注2：なお，積分と無限和の順序交換が可能であることを Σn=1,∞1/n² の値は、何になるのか？ これは、バーゼル問題と呼ばれ、1644年に ピエトロ・メンゴリによって提起され、1735年にレオンハルト・オ

フーリエ級数展開の問題です 画像の問３が分かりません 問１はa0 2 Yahoo 知恵袋

2

Vienādība ctgα = ctgβ ir spēkā tad un tikai tad, ja利用平方根来解下列方程(2x1)^2169=04(3x1)^21=0 1年前 1个回答 衣缺不补则日以甚下句是什么?二つの自然数が互いに素になる確率 6/π^2 も同様な方法で証明出来るのかなぁ。 ある一つの自然数が素数pを約数に持つ確率は1/p ある二つの自然数が素数pを約数に持つ確率は1/p^2 ある二つの自然数が素数pを約数に持たない確率は11/p^2

If Sum R 1 N A R 1 6 N N 1 N 2 For All N Gt 1 Then Lim N Rarr Oo Sum R 1 N 1 A R Is

Pdf A Short Elementary Proof Of S1 K 2 P 2 6

π / 2 rad τ / 4 rad Circumference C of a circle of radius r C = 2πr C = τr Area of a circle A = πr 2 A = τr 2 / 2 Recall that the area of a sector of angle θ (measured in radians) is A = θr 2 / 2 Area of a regular ngon with unit circumradius A = n / 2 sin 2π / n A = n / 2 sin τ / n Volume of an nball 不可以這樣寫啦 右邊又不收斂 sin x = xΠ(1 (x/nπ)^2), 這個product才會收斂 n>=1 in fact, 這等式對任意複數都成立 比較 x^3的係數 1/6 = Σ (1/nπ)^2 ==> Σ1/n^2 = π^2/6Article How to Compute Σ1/ n 2 by Solving Triangles October 08;

Aip Scitation Org Doi Pdf 10 1063 1

Stirling

Σ1/n^4(2n,n) は簡単な初等関数・特殊関数では表せないのですが，そこで必要となるのがポリログ関数を用いた積分表示です．たとえば，ジログ関数の特殊値が円周率π，黄金比φと結びつけられるという事実が知られています． L2(1)＝ζ(2)＝π^2／61Σ1／n^2＝π^2／6 だけでなく， 2Σ1／n^4＝π^4／90 3Σ1／n^6＝π^6／945 4Σ1／n^8＝π^8／9450 5Σ1／n^10＝π^10／ 6Σ1／n^12＝691π^12／95・ も求2部分积分法，看到 和 就应该想到部分积分法了 第一项在 积分出来是0喔 所以 得证 3 由于 套用2问的结论 原式得证 4对 分部积分 注意到后半部分是 和 然后把 和 拿到同一侧 对右侧的部分进行部分积分 整理得到 5利用数学归纳法证明 如果 成立的

Projecteuclid Org Download Pdfview 1 Euclid Jam

Www Math Harvard Edu Media Narayanan Modular Forms Thesis Pdf

 Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeThe sum from n=1 to ∞1年前 1个回答 当x>时,下面无穷小量中与X等价的无穷小量为?A 3x B sinX C ln(1x^2) D xsinX 1年前 悬赏5滴雨露 1个回答 call at call in call off call out的用法 1年前 1个回答

2

What S An Intuitive Explanation Of The Following Mathematical Fact Math Displaystyle Sum N 1 Infty Frac 1 N 2 Frac Pi 2 6 Math Quora

Start studying 92 convergences Learn vocabulary, terms, and more with flashcards, games, and other study toolsSemiconvergence exemple de (sin t)/t Série numériques rappels somme d'une suite arithmétique suites géométriques suites définies par récurrence, terme général exemple de Fibonacci somme d'une suite géométrique Rappels surVienādība tgα = tgβ ir spēkā tad un tikai tad, ja α=βπn, n∈Z;

Carma Newcastle Edu Au Jon Preprints Books Mbye Expbook Ii Pdf

2

 14As volume of specimen remain constant, A 0 × L 0 = A1 × L1 2 π 2 π 2 L1 d d 0 × L 0 = d1 × L1 ∴ = 0 4 4 L 0 d1 2 d d ∴ ∈= log 0 d = 2 log 0 1 d1 ∈1 = true strain for first extension 9 ∴ 2 log = 0091 8 6 ∈2 = true strain for second extension d 9 = 2 log 0 = 2 log = d1 Applying Hollomon equation, n σ1 = K∈1 σ積分と和が一致する例のつづき kを正の整数として ∫(0,∞) (sin x/x)^k dx = 1/2 Σn=1,∞ (sin n/n)^k dx aを√1の整数倍でない数としてMathematics taken over all branches of the logarithm, is a rational function, and use this to give a short proof of ∑1/n 2 =π 2

Basel Problem Wikipedia

Stirling

11/2 2 1/3 2 1/4 2 ・・・・・＝Σ n=1～∞ 1/n 2 ＝π 2 /6 （式2） これは、16年にヤコブ・ベルヌーイが提示したバーゼル問題への解答として、1735年にオイラーが発見した有名な公式です。A short elementary proof of Σ1/k 2 =π 2 /6 January 12;Il Pi greco è una costante matematica, indicata con la lettera greca (), scelta in quanto iniziale di περιφέρεια (perifereia), circonferenza in greco Nella geometria piana il viene definito come il rapporto tra la lunghezza della circonferenza e quella del suo diametro, o anche come l'area di un cerchio di raggioMolti libri moderni di analisi matematica definiscono il usando le

Fourier Series Sum Of 1 N 4 Pi 4 90 Sum Of 1 2n 1 2 Pi 2 8 Youtube

Solutions To Problems

 バーゼル問題の級数の収束先が π 2 6 \dfrac {\pi^2} {6} 6π2 であることの証明はいろいろな方法があります。 特に，サインのマクローリン展開および無限積展開を用いるオイラーの方法が有名です。 ここでは，大学数学の道具を使わず高校数学で理解 If cot^1(n/π) > π/6, where n ∈ N, then find the maximum value of n asked in Sets, relations and functions by SumanMandal ( 546k points) inverse trigonometric functionsNow π π π π3 Z 2 Z 2 A0 = 1 dx = and B0 = x2 dx = , 0 2 0 3×8 and so 2B0 π2 = , A0 6 Hence for all n ≥ 1 we have n X 1 π2 Bn 2 = −2 (5) k 6 An k=1 We now estimate Bn in terms of An to get a bound for Bn /An

07 Perfect Numbers

Basel Problem Wikipedia

2π Z∞ −∞ dxe −µ xe ikx= 1 √ 2π 0 −∞ dxe µxe−ikx ∞ 0 dxe− e → = r 2 π µ µ 2 k 12Problem 2 ConsidertwooperatorsndB,shownbelow,whereaandbarerealconstants A= a 0 0 0 −a 0 0 0 −a B= b 0 0 0 0 −ib 0 ib 0 1Leonhard Euler Matemático (1707 Basilea, Suiza, 17 San Petersburgo, Rusia) Leonhard Euler nació el 15 de abril de 1707 en Basilea, Suiza y murió el 18 de septiembre de 17 en San Petersburgo, Rusia Fue hijo de un clérigo, que vivía en los alrededores de BasileaIn this shortnote, a series expansion technique introduced recently by Dancs and He for generating Eulertype formulae for odd zeta values ζ(2k1), ζ(s) being the Riemann zeta function and k a positive integer, is modified in a manner to furnish the even zeta values ζ(2k) As a result, I find an elementary proof of ∑∞n=11/n2=π2/6, as well as a recurrence formula for ζ(2k) from which

Www3 Nd Edu Apilking Math Work Old exams Exams s14 Exam 3s14 solutions copy Pdf

Basel Problem Wikipedia

 バーゼル問題について 無限級数 ∑ n = 1 ∞ 1 n 2 = 1 1 2 1 2 2 1 3 2 ⋯ の値が幾らになるのかという問題は17世紀後半から18世紀前半の西洋数学界における大きな関心事でした。 これは「バーゼル問題」と呼ばれ、多くの数学者の挑戦を撥ね退けてきた難問作者 pretendbbs@lalalatwbbsorg ("Weak and only weak") 標題 Re Σ1/n^2 = (π^2)/6 時間 Wed Jul 23 14 作者 pretend (Nature Weak) 站內 pretend 標題 Re Σ1/n^2 = (π^2)/6 1 1 回答 数列の極限に関する問題 数列の極限に関する問題 Σ1/n^2=π/6 (n=1→∞) を示せという問題が出たのですが、まったく方針がわかりません。 PCでは回答しづらいと思いますが、お願いします。 数学 ・ 4,365 閲覧 1人 が共感しています

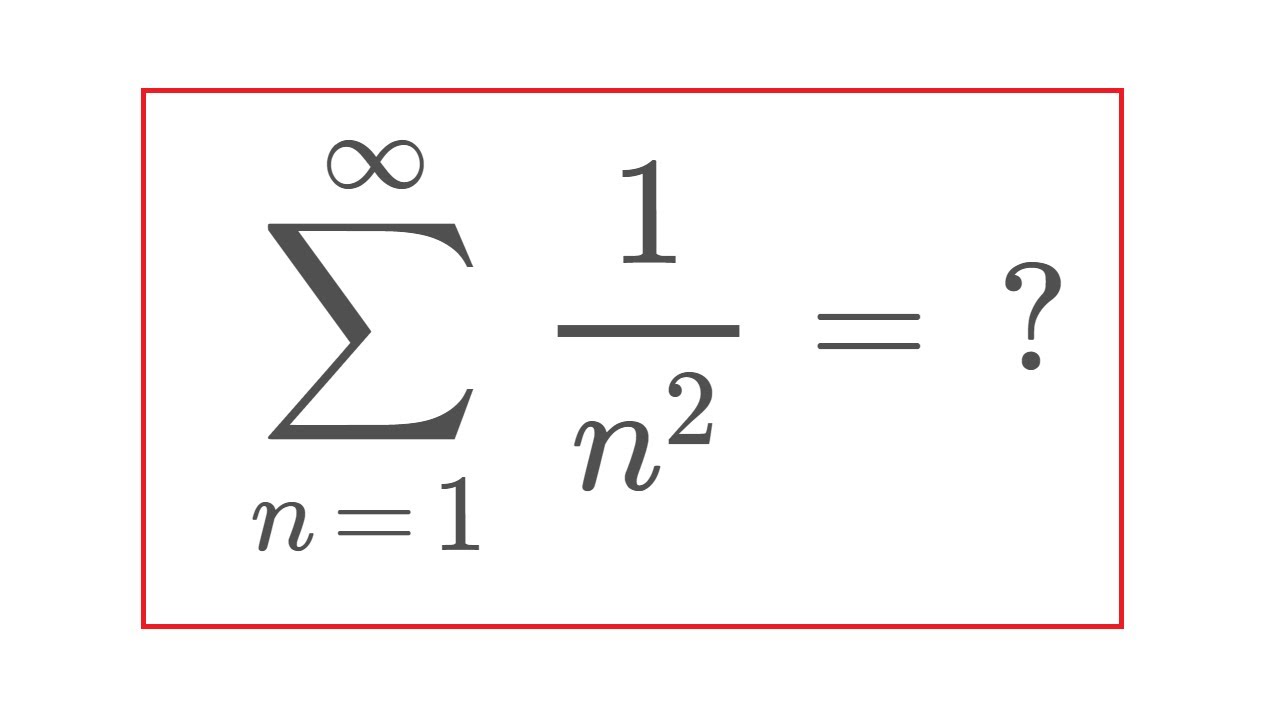
Sum Of 1 N 2 Youtube

黒木玄 Gen Kuroki 数楽 続き X 2 Log Sin X で同様のことをやると 実部から 0 P 2 Log Sin X Dx 3p 16 Z 3 P3 24 Log 2 が得られ 虚部 0から Z 4 P 4 90 の独立な証明が得られます T Co T2ikfjpenm

Solution for 6) Σ n ) Π 2" Physics Social Science

N Ceunes

Basel Problem Wikipedia

Electromagnetismo By Erika Machado Issuu

High Affinity Sigma 1 S1 Receptor Ligands Based On The S1 Antagonist Pb212 Future Medicinal Chemistry

Basel Problem Wikipedia

2

Chapter 2 Maths 3

2

The Sum Of The Series Sum N 1 To N 2 6n 10 2n 1 Is Equal To Sarthaks Econnect Largest Online Education Community

1

2

Shi396 Ch06

2

Fourier Series Sum Of 1 N 2 Pi 2 6 Youtube

Http Www Lmpa Univ Littoral Fr Smoch Documents M1 Gsi Probas Master1 Gsi Chapitre5 Pdf

Wallis Product Wikiwand

Oncertainarithmeticalfunctions Srinivasa Oncertainarithmeticalfunctions 177 What Is Remarkable About Pdf Document

Http Matwbn Icm Edu Pl Ksiazki 90 9016 Pdf

Integrale De Riemann Exo7

2

Semi Analytical Solutions Of Seismo Electromagnetic Signals Arising From The Motional Induction In 3 D Multi Layered Media Part I Theoretical Formulations Earth Planets And Space Full Text

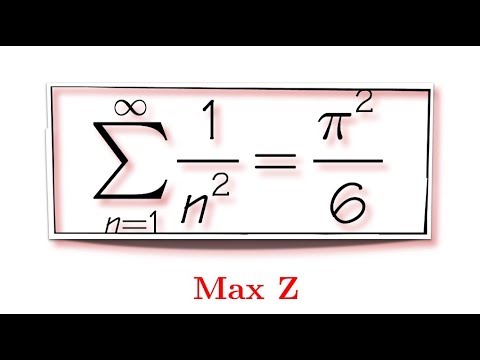
Proof By Intuition Done By Leonhard Euler Sum Of 1 N 2 Feat Max Youtube

2

2

蓑田恭秀 鉄緑会 En Twitter 早速今日の授業で話しました Rt Tonagai 仮面ライダービルド 第六話の話数を表す数式はバーゼル問題 S1 N 2 P 2 6 でした T Co 2w7s60mlpw T Co Iq5ecnnzlp

2

2

Pdf Some Results On Theory Of Infinite Series And Divisor Sums Nikos Bagis Academia Edu

Www Raco Cat Index Php Collectaneamathematica Article Download

2

Wc Saga Milyen Gyakran Proof 1 N 2 Pi 2 6 Laura Edwards Com

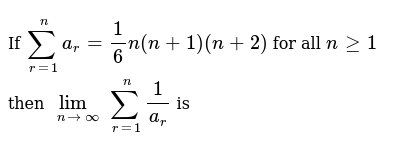
If Sum R 1 N A R 1 6 N N 1 N 2 For All N Gt 1 Then Lim N Rarr Oo Sum R 1 N 1 A R Is

Convergence Of Fourier Series Page 2

Pdf Another Simple Proof Of 1 1 2 2 1 3 2 P 2 6

8 2 Infinite Series Mathematics Libretexts

2

Vector Calculus Mathematics Statistics And Calculus Solution Manual Docsity

Www Jblearning Com Samples Students Solutions Manual Pdf

Testing The Convergence Of Sum Limits N 1 Infty Frac N Pi N E N 2 Mathematics Stack Exchange

Http Licence Math Univ Lyon1 Fr Lib Exe Fetch Php Media A12 Aga gfeuille3 12 13 Pdf

Http Www Ihes Fr Brown Irratmodulimotivesv8 Pdf

Osa Relations Of The Parameters Of The I K Distribution For Irradiance Fluctuations To Physical Parameters Of The Turbulence

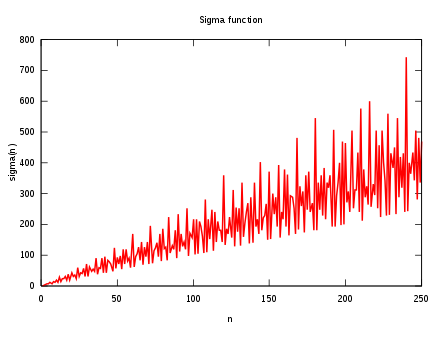
Colossally Abundant Number Wikiwand

Telescoping Series Video Series Khan Academy

9 Find The Following 3 9 27 S 1 16 64 2 2 Chegg Com

2

2

Pdf A Simple Proof That Z 2 Frac Pi 2 6

2

2

Exercices Suites Numeriques By Ech Charafi Adil Issuu

Emt4801 Tut102 For Year19 Memo 1 2 3 4 Pdf 1 Assignment 01 Emt4801 102memo 0 19 2 Solution To Question 1 I A Consider Un U N 1 N Nn It Course Hero

Arxiv Org Pdf 2101 003

1

2

多角度证明s1 N 2 P 2 6 谜镜 Fantasy 新浪博客

Www Normalesup Org Dconduche Prepas Pt Controles Dst1 15c Pdf

2

1

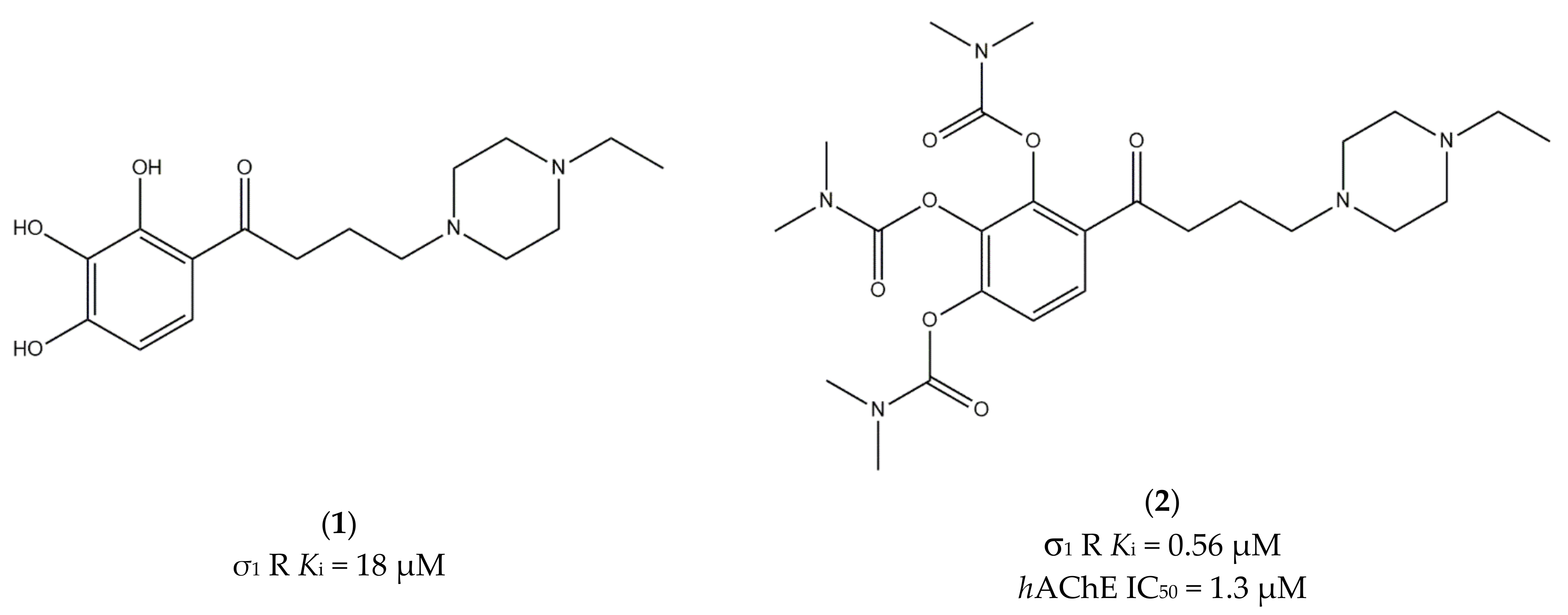
Ijms Free Full Text Multi Target Directed Ligands Mtdls Binding The S1 Receptor As Promising Therapeutics State Of The Art And Perspectives Html

What S An Intuitive Explanation Of The Following Mathematical Fact Math Displaystyle Sum N 1 Infty Frac 1 N 2 Frac Pi 2 6 Math Quora

Idents

2

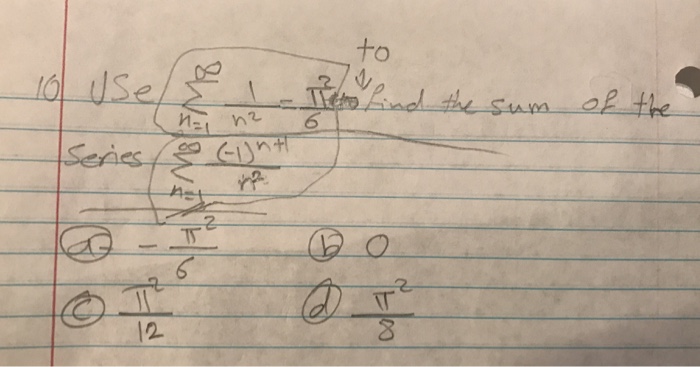
Use Sigma N 1 Infinity 1 N 2 Pi 2 6 To Find The Sum Chegg Com

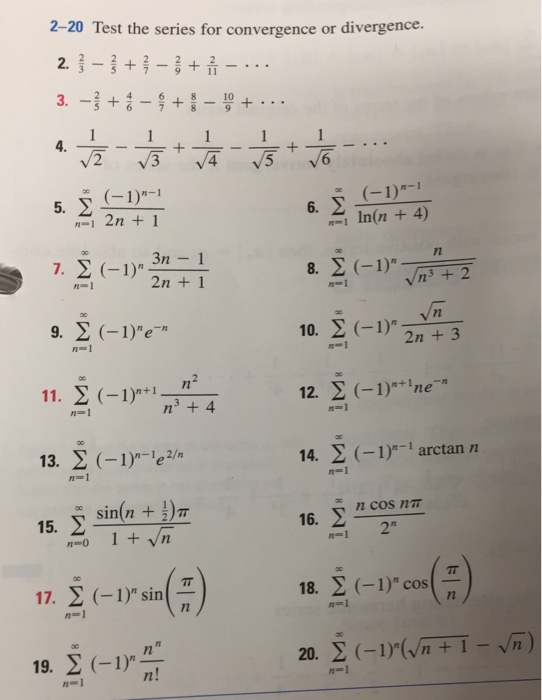
2 Test The Series For Convergence Or Divergence Chegg Com

1

Pdf A Short Elementary Proof Of S 1 K 2 P 2 6 Daniel Daners Academia Edu

Solutions Shigley S Mechanical Engineering Design 8th Edition Docsity

Http Mapage Noos Fr R Ferreol Atelecharger Textes Colles Pdf

Idents

2

Calameo Devoir 2 De Stt 1042 Uqtr

2

Given That Sum N 1 Oo 1 N 2 Pi 2 6 And Sum N 1 Oo 1 N 2 8n 16 Pi 2 A B Where A In N Youtube

The Value Of K 1 131 Sin Pi 4 K 1 Pi 6

2

2

8 2 Infinite Series Mathematics Libretexts

Http Champion Univ Tln Fr Agregation Interne Capescorrectionsujet07analyse Pdf

2

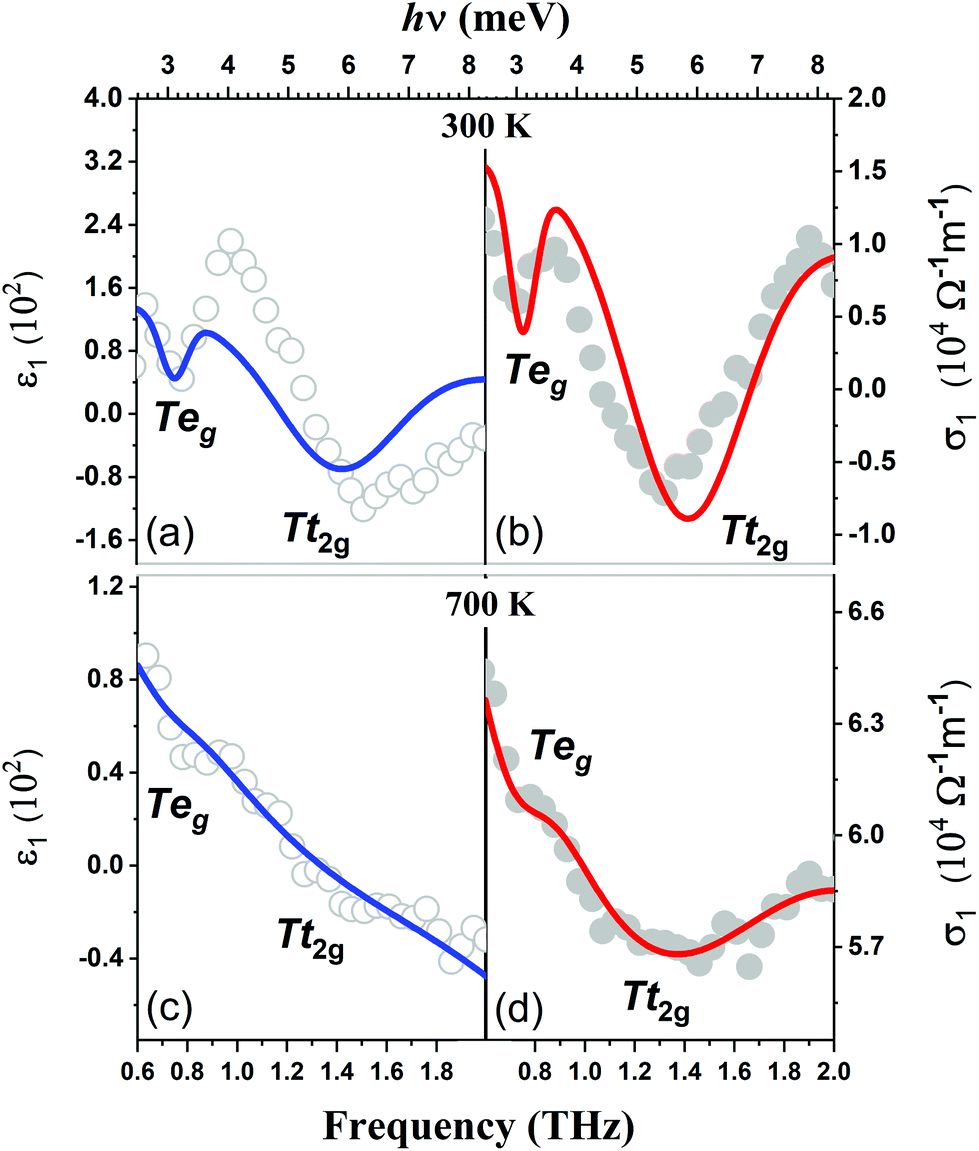
The Split Off Terahertz Radiating Dipoles On Thermally Reduced A V 2 O 5 001 Surface Nanoscale Rsc Publishing Doi 10 1039 D0nr038j

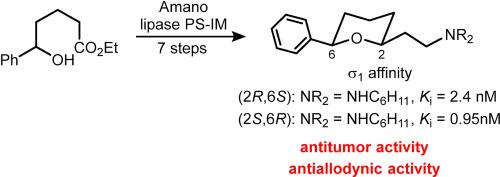
Chemoenzymatic Synthesis Of 2 6 Disubsttuted Tetrahydropyrans With High S1 Receptor Affinity Antitumor And Analgesic Activity European Journal Of Medicinal Chemistry X Mol

Incoming Term: σ1/n^2=π^2/6,